I know a lot of people have been waiting, patiently, for the most part, for my thoughts on the SP-10R. Well, perhaps not a lot, but at least one gentle nudge on a-gon every now and then. Please forgive the delay. It seems the one commodity I'm short on, which cannot be replenished, is time.
So, on with it I've seen units in the EU, both SP-10R and SL-1000R, come with wood flight cases. Mine didn't. I e-mailed Technics and the reseller I purchased my unit from why this was the case, but they neglected to respond.
I must admit I'm not a fan of the aesthetics of the 10R. I'm not talking fit and finish here, rather the industrial design. We have square buttons on the motor unit, round buttons on the power supply, square edges on the motor chassis and plinth, round on the armboard, etc. The left-justification of the controls on the motor as opposed to center-aligned with each other doesn't make sense to me either. It's like three separate people who never spoke designed each piece. I don't get it.
The brushed finish looks far better in person than in any pictures I've seen thus far. The platter finish is nice, however not as well machined as the MK3. Worlds apart here.


The 10R has tapped holes under the platter in the chassis that allow you to use the platter handles to drop the motor chassis in to a plinth. This is very handy, and something I wish the MK3 had. Unlike the MK3, the threaded holes in the platter of the 10R are not inset, so you have to be extremely careful when removing the handles to not drop them. Extremely careful. I was only very careful, and dropped one on my platter. I suggest holding them as I've pictured below during removal to be safe.


As is well explained on Technics site, the platter is a die-cast aluminum base with a brass top plate and tungsten weights, with a damping rubber underneath. Each platter is individually balanced, though I don't see in the literature if they specify static or dynamic. I do hope it's balanced with the damping material applied, as mine is quite a bit off, thought I doubt it'd matter much.




On my unit there's around a thousandth or two of wobble and axial runout. As the platter sits on three standoffs on the motor and has a tight fit around the spindle (as it should), there's no way to compensate. In the rare circumstance you ran across this on a MK3, you can easily change the relationship of the platter and spindle shaft to compensate.
Granted, these are all small nits and unlikely to affect how the 'table performs, but at $10K I don't expect to see such issues.
As I've several SH-10B5 plinths around, I decide to throw my 10R in one of them. No surprises here; everything fits as it should and bolts up fine. The armboard looks a little funny having a counter-chamfer to the motor chassis' square edge, but the gap is right and you hardly notice.
From here I let the motor run for about 72 hours, listening to some tunes as we went. I also did some measurements, which we'll talk about later. Note that my thoughts here aren't about what happened in the initial 72 hours - I've had this 'table since the end of May.
Let's get in to the fun stuff.
On the 10R, the brushed aluminum chassis, while serving as the mounting mechanism to a plinth, is more of an escutcheon as anything. The inner motor and outer chassis 'tub' are the main bodies of the unit.


Of course I took it apart. It's like you don't know me at all.
The back of the chassis, similar to the MK3, is a composite material. This is likely an evolution of TNRC, or some such. When you remove it, you think "damn, that's heavy", only to find two stainless steel weights inside. To be fair, this is a feature Technics calls out in their marketing literature.




The weights are 1.8kg and 416g.
There are plenty of pictures of the motor assembly around, so I can't be bothered to repost them here. Actually, I didn't take any pictures of the assembled motor. Yep, you know where this is heading.


As advertised, there are 18 coils, 9 each side, offset 60 degrees. The coils are wound very precisely, the board is quality, and the soldering is top-notch.


The bearing is your standard sintered bush with thrust pad setup. Same as the MKII/2A, the spindle is the shaft, and as such the same diameter. The thrust pad is floating, and of a thin polymer-type material. At the top of the bearing is a brass collar that the aluminum motor rotor hub attaches to.



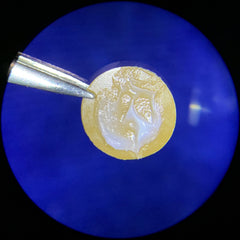


As advertised, platter rotation is tracked by an indexed optical encoder. I didn't count the slots. The magnified photo is 6x.


The motor movement has a nice, smooth heft to it. I spent quite a lot of time with the demo unit at the reseller's, carefully manipulating the motor. That one had a high friction spot in it, however, and thankfully, mine does not.
As is called out in the literature, the mounting plate that attaches the motor to the 'tub' is quite substantial.


Speaking of the 'tub', it's around 4.5mm thick and likely cause of an aluminum alloy. The casting looks quite good, as is expected in these modern times.


The 'brains' of the unit are contained within the motor unit itself. As with the the G/GAE, and I assume the GR, everything comes down to a single MCU, Technics apparent favorite being from Renesas. We've some circuity to read the encoder, and some circuitry to drive 3 push-pull amplifiers, and that's it. That's all you need.


Last, we come to the power supply, which is pretty much just a switching supply. The LCD and control panel is driven by a small uC, with a 2-wire interface back to the motor unit. Simple. Effective.


How does it sound?
Buy one. Find out.
Just kidding. Measurements-wise it edges out a couple of my MK3. I've done dozens upon dozens of measurements, in an endless circle of the slightest advantage going either way. I don't have a vibration-proof lab. That's the caliber of performance we're talking about.
Below, two polar plots. One from the 10R, the other from one of my MK3. Same test record, indexed off the start of the W&F track.
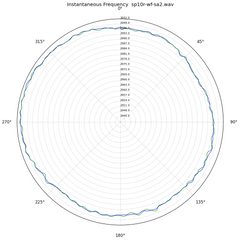
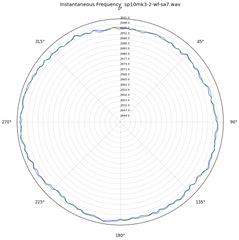
I'm not one for the purple prose of audio reviews. Sorry to let you down. I doubt my subjective observations bear much relevance to anyone else. I will say I could happily live with a 10R as my one 'table. Shiny, new, warranty, and performs great. What's not to like?
Would I trade a MK3 for a 10R? Not a chance. While objective measurements of the 10R are the slightest bit better than the MK3, I think the MK3 is a higher-caliber unit. Beefier components, better machining, and better industrial design; even if the control unit is dated. It's a brute.
]]>




































